Special Relativity Theory
Einstein’s 1. postulate implemented in the theory
Abstract
Einstein states in §1 in reference [1] that if we send a light from A to B, and reflected from B to A in a “stationary” inertial frame, of reference the time is the same each way, and we can calculate time from this as the distance AB divided by the speed of light shown as small “c” (AB/c). See reference [1]. According to Einstein’s 1st postulate in the start of §2, this time must remain the same in the inertial reference frame where A and B are located, even if A and B are in motion relative to other systems in the direction from A towards B. In §2, he states the time between AB which is in motion measured by a stationary observer when the light moves from B to A as rAB/c+v, where rAB is the length contracted distance and “v” is the system speed of A and B seen from a stationary observer.
This means as “v” is increased to approach “c” in the moving frame then time goes against zero in the stationary frame, but the time in the moving frame is constant! That means, that the faster the moving frame is moving the faster a clock must tick in the moving frame observed from the stationary frame. This is in direct contradiction to Einsteins §4, where he states a moving clock will tick slower with the Lorentz factor!
It will be shown that we have additional other problems when we try to implement Einsteins 1. Postulate in the remaining of the theory. See section 2 below.
–
I dare everyone – including Professors in Physics – but in general anyone that can understand Einsteins special relativity theory to find any errors in the following formulas, calculations or logic, and especially the conclusions. Please send this to: “stjerne” at “relativitytheory.eu.” See more at the end.
Download this whole text as a PDF file. Click here.
1. Introduction – Stationary and moving clocks
Let us use the same setup as Einstein introduces in his theory of special relativity reference [1], §1 and §2.
1.1 Description of a light signal in a stationary frame of reference
We start with 2 inertial frames of reference called ALPHA and BETA. ALPHA is included within BETA, and we have no movement between these 2 systems. They are both stationary compared to each other.
In ALPHA we have a point in each end as described in Einsteins §1 called A and B. See reference [1].
We assume that all is happening in vacuum, and that the distance between A and B is:
299.792,458 km measured to be the same in both ALPHA and BETA.
We now send a light signal from A to B and the light is reflected in point B and returns to A. See the setup in Figure 1. below.

Figure 1. – Example of Einsteins description in §1 in System ALPHA.
According to Einstein §1 the time for the light signal in ALPHA will be measured as the distance between the 2 points divided by the light speed (299.792,458 km/s).
This will mean that when we assume the distance from A to B being 299.792,458 km then a clock in ALPHA will tick 1 second while the light moves from A to B as well as the clock will tick 1 second while the light moves from B to A. As the 2 systems are not in motion a clock in in BETA will also tick 1 second while the light in ALPHA moves from A to B, as well as 1 second while the light returns from B to A.
1.2 Description of a light signal in a moving frame of reference
We now accelerate ALPHA inside BETA to a fixed steady speed of 0,6c. The speed of ALPHA will in BETA therefore be measured to: 299.792,458 km/s * 0,6 = 179.875,4748 km/s. See figure 2 below. This follows the setup that Einstein describes in §2 in reference [1].
According to Einsteins 1. Postulate in §2 then the clock must still tick 1 second each way in ALPHA, as
“The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems of co-ordinates in uniform translatory motion.” (Reference [1], §2 – Einsteins 1. Postulate).
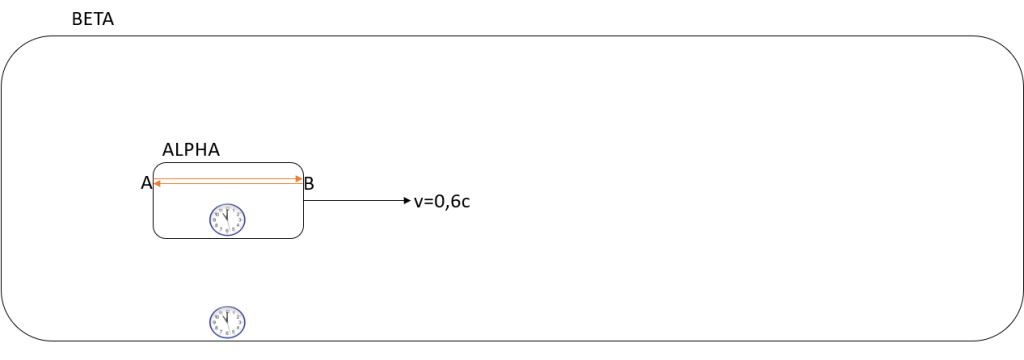
Figure 2 – Einsteins description in §2 with a specific speed of 0,6c of the moving frame (ALPHA).
Please note, that we cannot claim that it is BETA that is moving compared to ALPHA, as the assumption here is that we have no measuring of acceleration in BETA, but only in ALPHA.
According to Einstein §2 he specifies that the time seen from a stationary point of view the time will be two different times and can be calculated according to 2 formulas as he specifies at the end of §2 in reference [1] as:
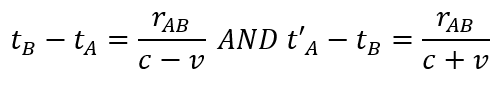
tB-tA is specifying the time (measured in the stationary system) while the light moves from A to B (time in point B minus starting time in point A). While t’A-tB specifies the time while the light moves from B to A (time when light returns to A minus the time in B when light is reflected). He specifies in §2, that the 2 formulas calculate time measured in the stationary system. He also assumes in §2 that the clocks that measures in point A and point B are synchronized correctly.
The value “rAB”is the length contracted distance between A and B in ALPHA, but measured in BETA and can be calculated according to §4 in reference [1] as the distance AB multiplied with the denominator in the Lorentz factor which he specifies in the end of §3 in reference [1] as:
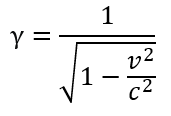
Where “γ” specifies the Lorentz factor – “v” specifies the speed of the inertial frame, and “c” is the speed of light.
This also means that instead of multiplying with above denominator we can divide by the Lorentz factor and calculate the length contraction as: AB/γ.
With a speed of ALPHA where v=179.875,4748 km/s (0,6c) we can calculate the Lorentz factor as:
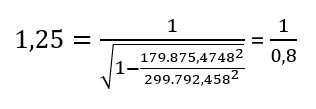
This again means that we can calculate the value of “rAB” as: 299,792.458 km / 1.25 = 239,833.9664 km (which equal 299,792.458 km * 0,8) which is the length contracted distance observed from a stationary observer in BETA.
Now we have the needed formulas and numbers based on the assumed distance between A and B and the assumed speed of ALPHA to calculate the time specified by Einstein with the 2 formulas as the stationary time in BETA as:
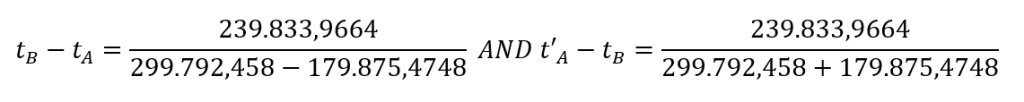
We then get the following values:
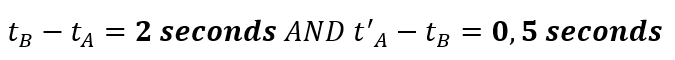
We can logically prove that Einsteins 2 formulas are correct as follows:
We have a starting distance of A to B of 239,833.9664 km measured in BETA and the system and thereby point B will move in 2 seconds with the speed of 179,875.4548 = 359,750.9496 km. After 2 seconds then point B will be 239,833.9664 km+359,750.9496 km = 599,584.916 km away from where point A was in the stationary system when the light signal was initiated. At the same time light will move 2*299,792.458 km = 599,584.916 km. This means that it is correct that the light will hit point B exactly after 2 seconds measured in BETA.
While the light must move from B to A which has a starting distance of 239,833.9664 km and point A will move towards the light, so the system and point A will move 0,5 second * 179,875.4548 = 89,937.7374 km towards the light signal and the light signal will move from B against A with 0,5 second * 299,792,458 km = 149,896,229. In total: 89,937.7374+149,896.229=239,833.9664. This means that the light moving from point B will hit point A exactly after 0,5 second.
2. Implementing Einsteins 1. Postulate – Conclusion
2.1 Outcome from the calculations in the introduction
According to Einstein §4, reference [1] a moving clock must tick slower than a stationary clock with the Lorentz factor. So, with the times calculated based on above examples, we can now create the following table with timing in seconds:
| Description | Stationary time §2 | Moving time 1. postulate | Moving time §2 and §4 |
| Time for light from A to B | 2 seconds | 1 second | 2.0/1,25 = 1,6 seconds |
| Time for light from B to A | 0,5 second | 1 second | 0,5/1,25 = 0,4 seconds |
From Table 1 we can now see that we have several issues regarding Einsteins 1. Postulate:
1. Two different claims for moving time
We have 2 different claims of what moving time in ALPHA is. According to Einsteins 1. Postulate a clock in ALPHA must tick 1 second each way (AB/c), but according to the claim in §4, then a moving clock will tick slower than a stationary clock with the Lorentz factor (Lorentz factor with v=0,6c is in this case = 1,25), and thereby we will also have 2 different moving times based on the two stationary times coming from the 2 formulas in §2 (giving us movement times of 1.6 second and 0,4 second). The 2 claims are in contradiction with each other.
2. Both clocks cannot tick in a steady pace
If the clock in the stationary system (BETA) ticks in a steady pace, then the clock in the moving system (ALPHA) must change pace based on Einsteins 1. Postulate, when the light is reflected from point B, as while light moves from A to B the moving clock ticks twice as slow (1 second versus 2 seconds) than the stationary clock, but is ticking twice as fast when light moves from B to A (1 second versus 0,5 second). That is not following normal physical laws.
3. Clocks must tick faster when system moves against the light beam
The ticks and clock speed while light moves from B to A will always be faster in the moving system versus the stationary system if we use Einsteins 1. Postulate. This agrees with the given calculated seconds based on the example distances in Table 1 above:
1 > 0,5
The seconds shown mathematically as:
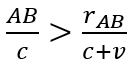
This is also in contradiction with Einsteins claim in §4, reference [1], that a moving clock is always ticking slower than a stationary clock. The stationary time will always be less than moving time independent on the distance or the speed “v” (while “v”>0) while the light moves from B to A.
Note: If we have multiple inertial frames moving in different speeds, then the time must according to the 1. Postulate remain 1 second (AB/c) in all the moving frames, but the higher speed each inertial reference frame has compared to the stationary system the faster a moving clock must tick in the reference frame in question, observed from the stationary system, while light moves from B to A!
4. Factor between clocks is not the Lorentz factor
The factor between stationary time and moving time using Einsteins 1. Postulate while light moves from A to B does not correspond to the Lorentz factor (but will always be slower), and neither the factor while light moves from B to A (as this will always be faster as pointed out in point 3 above).
Only the total time (2,5 seconds versus 2 seconds) corresponds to the Lorentz factor. This is in contradiction to Einsteins §4, reference [1].
5. Lorentz transformation does not support 1st postulate.
According to Einstein end of §3 in reference [1] then we can also calculate the moving time using Lorentz transformation, where we use stationary time, and the movement of the inertial frame measured on the stationary x-axis, where stationary time is shown as “ t ” and moving time is shown as “ t’ ”. The transformation formula then looks like this: t’= γ(t-v*x/c2). If we use the 2 seconds from A to B measured stationary, then moving time can be calculated as: t’= 1.25(2-179,875.4748 * (179,875.4748*2)/299,792.4582)=1.6 seconds. That gives of course the same result as t/ γ which is 2s/1,25 = 1.6s so moving time using Lorentz transformation is also in contradiction to Einsteins 1. Postulate
Obviously as we can see from table 1, and the 5 points above, when we try to implement Einsteins 1. Postulate in the remaining of his theory, then it shows impossible output. A moving clock will never be able to have a steady pace, and a moving clock when light moves against the moving reference frame direction will always have to tick faster than a stationary clock.
It is not possible for a moving clock to tick as described compared to a stationary clock if we try to accept Einsteins 1st postulate.
So, we can now conclude that Einsteins 1. Postulate is logically wrong (when we assume that the remaining of his theory and formulas are correct).
At the same time, we must also conclude that Einsteins §4 is correct so we will have 2 different moving times that will be stationary time divided by the Lorentz factor and with the examples above in Table 1 it will be 1,6 seconds for the light to move from A to B, and 0,4 seconds for the light to move from B to A.
2.2 A moving light clock
Now let us proof that a moving clock must tick differently and as Einstein described in reference [1] §4, while the light moves back and forth, and thereby also that Einsteins 1. postulate is wrong.
Let us assume the same setup as in the Introduction in figure 1 but in addition to a normal clock we also have a light clock that is 1/100 of the distance between A and B. Based on a measurement in both systems before we accelerate ALPHA.
Then the height of the clock must then be:
2,997.92458 km.
We send the light vertically in this clock (blue square) as shown in figure 3 below:

Figure 3 – ALPHA with a light clock (blue frame) and ALPHA and BETA is not moving compared to each other.
We have the same setup as described for Figure 1, except that we have now added a light clock that ticks 100 times per second in a stationary setup.
So, in this case, where ALPHA is not accelerated then the light clock must tick 100 ticks while the light moves from A to B and also 100 ticks while the light moves from B to A according to Einsteins §1 in reference [1].
In total 1 second each way as also described in regards to the setup shown with figure 1. If the 2 “normal clocks” in figure 3 also have 1/100 of seconds shown, then they will tick 100 times accordingly.
We now accelerate ALPHA inside BETA up to a fixed steady speed of 0,6c. The speed of ALPHA will in BETA therefore be measured to: 299.792,458 km/s * 0,6 = 179.875,4748 km/s. Note that also in this setup, then it is ALPHA and only ALPHA that has been accelerated up to 0,6c km/s. We measure no acceleration during the test in BETA. This is the same setup as described in Figure 2, but now with the additional light clock.
In this case the light in the light-clock must move a little longer seen from BETA to reach the top and bottom as shown below in figure 4 below:
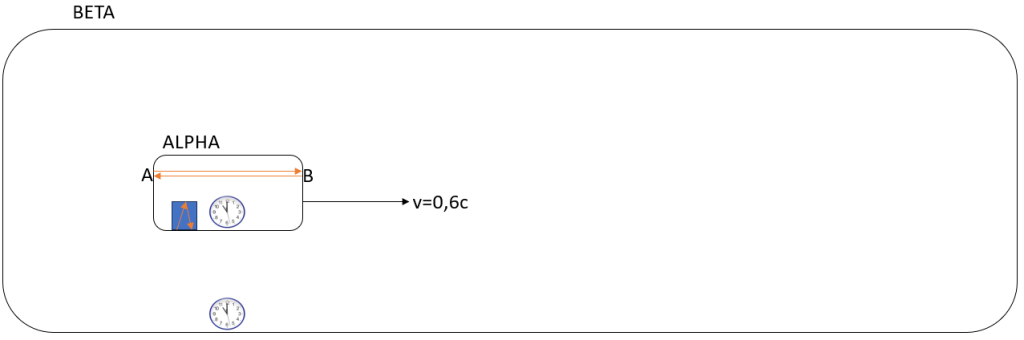
Figure 4. Light in the light clock is moving a bit longer seen from BETA
The light in the light clock is moving slantwise up and down seen from BETA because ALPHA is moving, which is the typical way that time dilation is shown visually. An example of this logic can be seen in figure 37.6 on page 1229 in reference [3].
We can now calculate the length seen from a stationary viewpoint of the light in the light clock using the Lorentz factor we have already calculated as 1.25 as:
2997.92458 km * 1.25 = 3,747.405725 km
As 3,747.405725/299,792.458=0,0125 second then when 1/100 second has passed in ALPHA a corresponding 1.25/100 second has passed in BETA, and shows that the km calculated length of 3,747.405725 km is correct under the assumption that a moving clock ticks slower than a stationary clock with the Lorentz factor as Einstein has stated in §4 in reference [1], and also again as described in figure 37.6 on page 1229 in reference [3].
We have already calculated stationary time from A to B as 2 seconds and from B to A as 0,5 second, according to Einsteins 2 formulas found last in §2 in reference [1] and shown in Table 1, so now we can calculate the length of the light between these 2 points measured in the stationary system in BETA as:
Light from A to B in km = 2.0 * 299,792.458 = 599,584.916 km
Light from B to A in km = 0.5 * 299,792.458 = 149,896.229 km
And now we can then calculate how many ticks the light clock must tick seen from the stationary system BETA as follows as the total length of the light in the light clock and the light moving between the 2 points A and B must be the same (measured in BETA) as light moves with equal speed:
Light from A to B in light-ticks = 599,584.916 / 3747.408725 = 160 ticks
Light from B to A in light-ticks = 149,896.229 / 3747.408725 = 40 ticks
In conclusion then the light in the light clock must tick up and down 160 times which equals 1.6 seconds while the horizontal light moves from A to B corresponding to 2 seconds in the stationary BETA, and likewise 40 times up and down which equals 0,4 second while horizontal light moves from B to A corresponding to 0,5 second in the stationary BETA.
This light clock example is the ultimate proof that when we have 2 different stationary times, then we will also get 2 different moving times that is slower than stationary time with the Lorentz factor. Einsteins 1. Postulate is wrong, and his claim in §4, that a moving clock ticks slower with the Lorentz factor is correct.
This inconsistency has been present in the theory (reference [1]) since it was first published in 1905 (in German language).
Unless we try to implement parallel universes then there is no way that the light clock in the moving frame can be seen to tick 100 times up and down for the same experiment observed in the moving reference frame ALPHA. The “normal clock” will then also have ticked 1,6 seconds while light moves from A to B (light clock and normal clocks shows same pace), and 0,4 second while light moves from B to A.
This is a proof that without doubt shows that Einsteins 1. Postulate is wrong unless someone will start to say that Einsteins 2nd Postulate (see start §2, reference [1]) is wrong and that light have different speed and influenced if it is initiated vertically versus horizontally in regards of the moving reference frame.
Please also note that the number of ticks in the moving frame is “observed” from a stationary observer and compared to the number of ticks in the stationary frame of reference also observed by a stationary observer. This means that we cannot use “relativity of simultaneity” to “explain” the problem, as this phenomenon is only claimed between 2 different observers in motion to each other.
In general, then it is obvious that if light moves with the same “light speed”, and we have 2 different stationary times, then we will also have 2 different moving times using light clocks.
Only way to get “the same time” each way in the moving frame is if “light changes speed” up and down from when the horizontal light moves from A to B versus from the horizontal light moves from B to A.
We have the same issue here, that a clock must change pace during the test, which is independent of what type of clock we use. It is logically impossible to claim that we can have 2 different stationary times, which both shall equal one and the same time in a moving frame, unless the moving clock changes pace, and then it is not a really a clock that can be said to be valid to measure time after all.
3. Objections to the conclusion
3.1 General
The above problems are coming directly from the theory itself. According to Einsteins 1. Postulate a clock in the moving reference frame must tick as described and not change regardless of speed compared to a stationary observer and notice that we have assumed that it is the moving frame that has been accelerated, so no one can argue that the relative speed difference of 0,6c is coming in full or partly from the stationary reference system BETA. This will be discussed in more details in point 3.5 below.
Likewise, the stationary clock is based on the 2 formulas that Einstein specify in §2.
The ticks and thereby the time of the moving clock and the stationary clock is therefore based on direct statements on how the clocks / time must be from the theory and not based on assumptions regarding different observers or other indirect assumptions.
Never the less, as this is a direct attack on the relativistic paradigm developed by Einstein that has been accepted for more than 115 years, then we shall go through some specific known objections in the following.
3.2 Relativity of simultaneity
The issues cannot be explained by e.g. claiming that this is simply a matter of “relativity of simultaneity”, as the claims are direct coming from the theory on how clocks shall tick, and not different views of specified observations of observers in different speed as described in point 3.1.
We can also as Einstein did in §4 in reference [1] claim that both the moving clock and the stationary clock are observed by a stationary observer, and then we cannot use “relativity of simultaneity” as explanation to the above issues as “relativity of simultaneity” is only claimed to be observed between different observers moving relatively to each other, as described earlier.
The description of the light clock is a situation where we see how many ticks the moving light clock per definition must tick theoretically but also calculated from a stationary view point compared to the time of a stationary clock.
This example can therefore not be explained using “relativity of simultaneity”.
3.3 Time is different in each end or clocks are not synchronous
Some might object and say that the “time is different” in each end of the moving reference frame. However, such statement is in direct violation with the 1. Postulate. If a clock in one end of an inertial frame of reference is ticking with a different pace than a clock in the opposite end then the physical laws of change is different not only between inertial frames but also inside inertial frames. Such an “explanation” would be in violation with the relativity principle. Not only the classical principle but also Einsteins extended principle that include electromagnetic radiation.
Also, if light moves with the same speed in all cases, then 2 light clocks must tick with same speed in each end of an inertial frame of reference. So, no sense in claiming “different times” in each end of an inertial frame of reference.
Secondly then Einstein claims that you can synchronize 2 clocks in each end of a stationary inertial frame in the start of the special relativity theory in §1, and he also assumes that 2 moving clocks are synchronized in §2 according to his specification in §1. Saying that time can and must be different to “explain” the mentioned issues makes then no sense, as this would be in contradiction to Einsteins theory and as just described it makes no sense to say that the moving clocks are not synchronized as this is an assumption that Einstein describe as a starting point of the example of the moving reference frame in §2.
Please also note, that we do not discuss a situation about synchronized clocks in the moving reference frame versus the stationary reference frame. We do not discuss how we measure the time with synchronized clocks, but only how many ticks a clock (one single clock) in each reference frame must tick if we compare Einsteins 1st postulate saying one and the same time each way, with Einsteins 2 formulas in §2 in reference [1] saying 2 different times. We are simply accepting that the measurements using the clocks as described by Einstein are correct in both situations, and then we take the consequence of Einsteins formulas and postulate and shows that we have a logical problem.
The starting points of the clocks while the light moves back and forth does not matter in regards of the problem. All that matters is how many ticks a clock in the moving system must tick according to Einsteins 1. Postulate versus how many ticks a clock in the stationary system must tick for the same event from a theoretical point of view.
Each clock can have whatever and different starting points and be out of sync as that does not matter. Only the theoretical number of “ticks” are in question here.
So, arguments about “different times in each end” and a-synchronous clocks have no bearing in this case.
3.4 Relativistic doppler effect
Einstein describes in §4 that a moving clock will tick slower with the Lorentz factor than a stationary clock “viewed from a stationary observer”, and this factor is only deducted by the speed of the moving frame of reference, and no other factors are mentioned. So, we cannot claim that other factors must be included e.g. relativistic doppler effect, unless we at the same time says that Einsteins claim in §4 is wrong.
We cannot use “relativistic doppler effect” as explanation for the problem as we could make the same setup where we do not send any light between the points, but just have a moving clock and a stationary clock. If we have a stationary clock that shows 2 seconds, then the moving clock must according to §4 tick 1.6 seconds (2/1.25=1.6) if the moving frame has a speed of 0.6c, and not 1 second so it makes no sense in this situation to talk about “relativistic doppler effect” as explanation that it is not 1.6 seconds and 0.4 second each way, as we in this situation do not have light involved at all. No light signal – no possibilities to explain the problem using “relativistic doppler effect”.
How a light signal should affect the speed of a clock to tick faster or slower is also not explained by just saying that we need to adjust for relativistic doppler effect.
Even if we accepted that we should adjust the 1,6 seconds to 1 second and 0,4 second to 1 second, then this would still not explain that a clock in the moving frame then should change pace while light is moving back and forth, and will not explain that the moving clock must tick faster than a stationary clock when we send light against the direction of the moving reference frame.
Relativistic doppler effect is coming from the measured wavelength and amplitude and the clock that measure this is affected by the speed, but the clock that measures this is not physically affected by the light wave. So Relativistic doppler effect does not have any effect on a clock tick.
Last but not least, then the speed of light and the length of the light that moves as described in point 2.2. where we measure time using a light clock cannot be explained with relativistic doppler effect. The observed waves are not changing the theoretical calculated ticks in point 2.2. above.
3.5 How can we know that BETA is not moving
Some might claim that we could just as well say that it was BETA that was moving, and not ALPHA, but that has already been taken into consideration in the setup of the description and the assumption, where we have ALPHA and BETA not moving compared to each other, and then we assume that we accelerate ALPHA up to a steady speed of 0,6c inside BETA. In this case, we cannot claim that the speed difference is coming from BETA, as the full speed difference comes from ALPHA’s acceleration! The assumption is that we cannot measure any acceleration in BETA during the experiments.
Some might then say that we cannot tell if BETA and thereby also ALPHA meaning both systems might be moving compared to the remaining universe in the starting point as described in Figure 1.
However, the assumption in Einstein’s special relativity theory is that any inertial frame of reference can be seen as “stationary” or “at rest”, and that everything else is moving compared to the rest frame. This is also the assumption that Einstein make in §1 in reference [1], and he claims in this first chapter that when we have a “stationary” inertial reference frame, then the time moving from A to B equals the time for the light moving from B to A.
Einstein do not claim that we can say that a reference frame is moving. He claims that we can see any inertial frame of reference as at rest.
Secondly, let us accept the assumption that both ALPHA and BETA is moving in the direction from B against A, and let us assume that they both move with the speed of 0,6c (compared to the remaining of the universe). If we in this setup still accept, that Einsteins assumptions are correct, then as neither system is moving compared to each other, then we should measure 1 second for the light moving each way in both systems (that makes no sense compared to what we found out in table 1 above, but let us still assume this). We now accelerate ALPHA up to a speed of 0,6c in the direction from A to B, basically meaning that ALPHA is deaccelerating compared to the speed of both systems in the opposite direction and ALPHA is now stationary. But in this case, then according to Einsteins 1. Postulate the time in ALPHA should still be 1 second each way, but in BETA it should read 2 seconds and 0,5 seconds, as it is ALPHA that is moving (has measured acceleration), so we should have the same numbers as in Table 1. Then we still have the same inconsistency.
A clock in ALPHA cannot tick with a steady pace in this setup either.
The sticking point in the whole setup is that if we measure the same time both in ALPHA and in BETA of the light moving from A to B as from B to A while ALPHA is not moving inside BETA, then we will measure 2 different times in BETA when ALPHA is moving inside BETA according to Einstein §2 reference [1] as described by his 2 formulas, and then we have the issues as shown in table 1 and the descriptions in the following in point 2.1 as described earlier. If we do not measure the same time from A to B as from B to A, then we are in contradiction to Einsteins §1 and in general to his 1. Postulate in §2 as described in reference [1].
So, claiming that BETA and thereby ALPHA is moving in space would contradict with Einstein’s theory (reference [1]). See also the example last in point 4.2 below.
4 Conclusions
4.1 Einsteins 1. Postulate – Relativity principle
Einsteins 1. Postulate that includes electromagnetic radiation in the relativity principle is wrong.
Electromagnetic radiation can be measured to be different each way – if we can synchronize our clocks correctly – if the inertial frame of reference is moving compared to a light beam.
This also means that we must give up other central points derived from the theory in addition to the relativity principle. See the following points.
4.2 An absolute stationary inertial frame of reference and movement in space
We can now define an absolute stationary inertial frame as follows:
An absolute stationary inertial frame of reference does not move compared to the universal point from which a light beam has been initiated inside the frame.
This can also be described as:
An absolute stationary inertial frame does not move compared to the moving light beam. It does not move against or away from a moving light photon in any direction at any time while the light photon is moving in the universe. As a light photon is moving independently of an inertial reference frame, it does not matter if the light photon has been initiated inside or outside the frame.
This means that the universal light path from a light source inside an inertial frame sending light in all directions will be the same universal distance as well as measured distance inside the frame if the frame is absolute stationary. If, however the frame is moving away or against a moving light photon, then the distance inside the frame might be measured the same both ways, but the universal distance will be different, and that is why we will measure 2 different times from “a stationary” viewpoint, but also will measure 2 different times in the moving reference frame (even though the moving clock will tick slower than the stationary clock with the Lorentz factor).
In our first setup in Figure 1, we have a description of a “stationary” system. This system will be absolute stationary if it does not move against or away from the front of the moving light beam. If it is absolute stationary, then the time will also be the same each way. However, if the system is moving, in the universe then the time will be different for the light moving each way as the universal light path will be different each way. A moving light clock will also show 2 different times as proven previously.
Even though it might be difficult or even impossible to identify the “universal point” from where a light beam has been initiated then this universal point from where the light signal was initiated must exist theoretically.
If an inertial frame has been accelerated then it is also “moving in space” and the universal point from which a light signal has been initiated will in this setup per definition be different from the point identified within the frame itself. The universal light path will then change depending on how the frame moves compared to the light beam, and it will be possible to measure as changes in measured moving time as proven above.
We cannot just postulate that objects move in the universe “since the start of the big bang”, and always have done this without having been accelerated at some point in time or accelerated when big bang happened. If we had expansion of the empty space without any physical matter or radiation placed in this universe, then we could not be able to talk about movement (and not time either) in this universe. If we had physical objects that just “expand with the expansion of the universe”, then there would not be any displacement of these objects compared to each other either. If we had a virtual ruler between 2 objects that had 100 marks with equal distance between each mark, and the universe expands including the virtual ruler then we would measure no movement between the objects. Only way to measure movement of objects would be if they changed relative position to each other, and this could then only happen if they actually had measurable acceleration.
We cannot just calculate speed of a light beam in a moving inertial frame as the distance of the light beam within the frame divided by time. If we take the 1,6 seconds for the time of the light moving from A to B and a measured distance of 299,792.458 km inside ALPHA then the speed of light would be calculated to (299,792.458/1.6): 187,370.2863 km/s.
This shows that the claim that light moves with a constant speed based on a measured distance within an (moving) inertial frame of reference is wrong and we instead can conclude that the system wherein we measure is moving, and that we can calculate our speed compared to an absolute stationary frame of reference.
Note that Einsteins 2. Postulate in the start of §2, reference [1] can still be correct as this says:
“Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body.”
This statement is just saying, that in a (complete) stationary system we measure the light speed to be the same independent of the light is emitted from a stationary or moving source. That is not in contradiction with anything else in the theory, except that we here accept that the system must be absolute stationary. The 2. postulate stated above is just saying that a light photon does not possess any inertia and that the speed in the universe then is unaffected by the speed of the light source. It is also claiming as nothing else is mentioned, that a light photon is moving with its maximum speed from when it is initiated without any needed acceleration.
If we have truly synchronized clocks, then we can calculate our absolute speed of our inertial frame of reference where we can take the numeric difference between the theoretical time which with the given distance in our example should be 1 second to the measured time which is 1,6 second or 0,4 second (depending on the direction).
Numerical value we can call tval are in both cases 0,6 second.
We can now use the following formula to calculate our absolute speed where AB is measured distance of the light movement between the 2 points A and B measured in our moving frame:
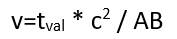
This will then with our previous example distance and speed of 0,6c be:
179,875.4748 km/s=0,6 * 299,792.4582 / 299,792.458
We have to completely change the view on how to look at “movement”, compared to the relativistic view point of Einstein and relativistic philosophers before him.
It makes no sense to say, that all inertial frames of reference can be looked upon as if they are “at rest”, and all other objects are moving compared to this rest frame. An inertial frame of reference that previously has measured an acceleration will per definition be moving compared to space / the total universe until a corresponding deacceleration has been measured and if this frame has been accelerated up to a fixed and steady speed compared to the remaining of the universe then it cannot be said to be “at rest”.
See also point 4.4 below regarding symmetry between inertial frames. This has nothing to do with the concept of “ether”, but is a logical deduction of “movement in space”.
This means that ALPHA and BETA in figure 1 might or might not have been accelerated previously and therefore might be or might not be moving in space, but there is no doubt that in our example we have the assumption that ALPHA is accelerated compared to BETA as described in Figure 2.
Let us again make the assumption, that both ALPHA and BETA at the starting point actually is moving in space in the direction from B against A with a steady speed of 0,6c compared to the remaining universe, but not moving compared to each other. If we then measure the time in BETA for the light moving from A to B in ALPHA (where B is moving against the light with 0,6c), then Einsteins §1 says the time in BETA should be AB/c which would be 1 second as both systems are at rest compared to each other, but as point B in this theoretical setup is racing towards the light with a speed of 0,6c (seen from a universal stationary perspective), then the time will actually be measured to 0,4 seconds in BETA. The reasoning is according to the theory, that both ALPHA and BETA is moving compared to the moving light signal and is not at rest compared to the universal point from where the light signal has been initiated. Both ALPHA and BETA must then be length contracted compared to “the remaining universe” with the Lorentz factor, so seen from this “stationary view point” then stationary time would be measured to rAB/c+v which would give 0,5 second, and then as the moving time goes slower with the Lorentz factor, then moving time would be measured to 0,4 second in both ALPHA and BETA. However, the theory would say 1 second each way, so an observer in BETA would then be able to conclude not to be at rest, but also that the observer is moving in the direction from B towards A, and would be able to calculate absolute speed to be 0,6c using the formula above.
4.3 Relativity of simultaneity
As we cannot use reference points in a moving inertial reference frame to measure correct universal light path, then Einsteins claim of relativity of simultaneity based on this principle is wrong as well.
In section VIII in reference [2] Einstein describes a situation where 2 lightning events happens in 2 different points that he calls A and B along a railway line. He defines that the 2 lightning events are simultaneous if an observer in the midpoint between the 2 points receive the light from each point at the same time.
However, as Einsteins 2. Postulate (§2, reference 1) says: “Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body.”, then light is moving independently of the inertial frame, and this means, that if the frame is moving compared to the moving ray of light, then we cannot use neither reference points within the reference frame nor the length between these reference points to calculate the universal length of the moving light.
This is never the less what Einstein is doing in the above example in section VIII. From the description is sounds like the events are happening on Earth (along a railway line), but Earth is rotating around itself, and around the Sun, and the whole solar system is rotating around a black hole in the middle of our galaxy, so the two points A and B where the lightning hit the railway line are moving and the observer too in the universe after the ray of light has left the two points, meaning that the universal light path from each universal point and to the observer will be different. Even though he is called “stationary” observer at the railway bank.
So, we have to extend the definition as described in VIII in reference [2] on how to measure simultaneity between 2 events in 2 separated universal points in the universe as:
Two separated events in the universe are simultaneous if a light signal is initiated when the event happens in each universal point, and the two light signals arrives at the same time to an observer when this observer is exactly the same distance to each of the two universal points. Light signals must travel without or with the same influence from gravity.
When it here and in point 4.2 before refer to a “universal point”, then it is a point that is absolute unique in the universe and can only be measured compared to a “universal grid”, and not to an arbitrary chosen inertial frame that might be moving compared to the light beam. If a light photon has been send out from a point in an inertial frame and this frame is moving compared to the light photon while the light photon is moving, then we will never measure the correct distance (universal distance) of the moving light photon within this arbitrary chosen inertial frame!
CONCLUSION: You cannot use reference points in an inertial frame of reference that moves compared to a light beam to measure the correct length of the moving light beam.
We need to say that we have to be exactly the same distance to the 2 universal points when we receive the signals, and not any points in an inertial frame that might have moved (and maybe the observer too) while the light signals were on their way to the observer. If we do not have a universal reference frame with reference marks, then it might be difficult or even impossible to identify the 2 universal points from where the light originally initiated in the total universe, but that does not change the fact that these theoretical points exist.
The light sources that initiated the signals can also move away from the universal point after the signals has been initiated, so a star that has emitted a light signal cannot be used as a reference point if the star is moving compared to space/universe.
In section IX in reference [2], Einstein then describes the same example but where the 2 lightning are happening in each end of a moving train with an additional moving observer exactly in the middle of the train, and he then concludes, that the observer in the train will say, that the 2 signals were not happening at the same time as the observer in the train is rushing against the light in the front of the train and away from the light in the end of the train, while an observer at the railway bank will say they were simultaneous. Both observations should be equally valid according to Einstein.
However, this is obviously wrong. The moving observer in the train is not measuring correct universal light paths. The moving observer is using points in the “train reference frame”, which cannot be used to identify the universal points. The universal light path from the frontend is shorter than the universal light path from the backend, and that is why the observer receives the light signals at 2 separated times. The observer in the train does not fulfill the extended definition to speak about simultaneity, as the observer is not exactly between the 2 originally universal points of light initiation when signals are received. The observer in the train cannot use both ends of the train as reference marks of the light path, as these two marks as well as the observer is moving while the light is moving independently of the train movement (here we assume the idea, that the railway bank observer is absolute stationary).
There cannot be 2 or more equally valid viewpoints of simultaneity depending on the inertial frame of reference but only one that uses the original universal points from where the light was emitted as described in the new definition above.
If 2 different observers are exactly the same distance to 2 different universal points from which light has been initiated, then they will also agree on the observed simultaneity. The distance from the 2 universal points and the observer must therefore be measured from a universal perspective and not relative to an inertial frame that might be in motion compared to the light beams.
The observers can also be in different speed compared to each other as long as they are exactly the same distance to the 2 universal points at the time when they receive both signals.
All examples given in textbooks including Einsteins train example (Chapter IX, Reference [2]) as described above, books, compendiums, articles e.g. that show “different but equally valid views on simultaneity” are as Einstein wrongly using different inertial frames as reference of each view, where at least one of these inertial frames and thereby the observer do not have the same universal distance to each point of interest. At least one of the observers will not have the same universal distance to the 2 points of interest, and thereby the light signals will travel different universal distances, and in this case, it makes no sense to speak about simultaneity.
4.4 Symmetry between inertial frames of reference
Einstein also claims that we have general symmetry between 2 inertial frames that has a relative speed between them. The symmetry should be based on the relative speed between the 2 systems and should create both symmetry of time and symmetry of length contraction as he describes in §4 in reference [1].
As Einsteins 1. Postulate is wrong, then we do not have general symmetry between inertial frames of reference.
We can only have 2 situations of symmetry between 2 inertial frames of reference:
- The 2 systems are at rest compared to each other
- The 2 systems are moving compared to each other but have undergone equal acceleration.
In the 2 situations above then both time and length contraction will be equal in both systems.
In all other situations the 2 systems will not have symmetry, and in this case both the clock speed and the length contraction will depend on each systems undergone acceleration compared to an absolute stationary system.
Note that even in case of 2 systems have undergone equal acceleration then the clock speed as well as length contraction is not based on the relative speed difference between the 2 systems (the total speed difference between the 2 accelerated systems), but based on half the relative speed difference, as this is each system actual accelerated speed compared to an absolute stationary inertial frame of reference.
4.4.1 Twin paradox and acceleration
This also explains why we have what has been called the “twin paradox”. This paradox is explained starting on page 1232 in reference [3]. It says, that one twin called Eartha is staying on earth while the other twin called Astrid is send on a high-speed trip through the universe. If we had symmetry between the twins then both could claim that the other twin’s time is going slower. However, the claim is also, that Astrid should be younger than Eartha when she returns back to Earth. The explanation to this paradox is in reference [3] that Astrid had undergone acceleration. Therefore, we have not symmetry in the setup. So the explanation is actually stating, that we rarely have symmetry, and that we cannot just say that we have symmetry in general between 2 moving frames as Einstein did in §4 in reference [1].
This explanation is just saying the same as claimed in this paper. Astrid and Eartha have not undergone equal acceleration and Astrid is by default in the example seen to be moving faster through the universe than Eartha. Because of this higher speed of Astrid, then Astrid’s time has gone slower than Eartha.
It is not the acceleration time (time while Astrid is changing speed) that explains the total time difference. The acceleration and possible deacceleration is only a very small part of the typical time difference, so it is not the acceleration in itself that explains that we do not have a paradox, but the fact that we in general have a higher speed of Astrid than Eartha compared to the total universe in the described example.
This explains why we only can have symmetry of 2 moving frames when both have undergone exactly same amount of acceleration compared to a complete stationary frame.
This example also shows us that the claim that we have general symmetry between 2 moving frames and the symmetry is based on the relative speed between the 2 frames is wrong. If a rocket flies by Earth with 0,5c speed, then Earth is not length contracted by this factor.
We would not have had the formulation of the “twin paradox” in the first place, if Einstein had not claimed general symmetry in §4 in reference [1].
It should also have been obvious to all that have used “acceleration” of the traveling twin as explanation to the paradox, that this explanation is actually a contradiction to Einstein’s claim of general symmetry to all inertial frames independently of how the relative speed difference originally have occurred, and that the theory then must have a flaw.
4.5 Einstein synchronization of clocks using light signals
Last central point is that we cannot synchronize 2 clocks in a moving frame as Einstein claimed based on his logic from §1 unless we are absolute stationary. The claim has until now been that you could measure the time of a light beam as the total time from a light is initiated from point A and reflected from point B to it return back to A, and then divide this time with 2 and then an observer in point B could “synchronize” the clock by taking the time from Point A send using a light signal to B and add this calculated “half time”. This can be done in an absolute stationary frame of reference but not in any inertial frame that has been accelerated from this stationary setup.
This is as we have now found out an incorrect methodology. The time is not 1 second each way as described in the examples previously when the system is moving with 0,6c. Time is with the given distances and speed 1,6 seconds from A to B and 0,4 seconds from B to A measured in the moving frame. This means that differences between 2 clocks can come from both the speed of the system as well as asynchronous clocks as starting points, and if we do not know our speed then we do not know how much we shall adjust one of the clocks. If we were moving with 0,6c compared to an absolute stationary situation, and we tried to synchronize our clocks as described by Einstein, then we would implement a 0,6 second difference between the clocks, compared to an absolute stationary frame of reference.
There is no way to send a light from one point to the other and synchronize the clocks, as we do not know our absolute speed, and we can only measure that using synchronized clocks. This is a deadlock situation.
It does not change if you send the light in a circle or a square or one or more indirect points before the light returns to sender. The extra or less universal light path moving away from the initiating point because of the movement of the inertial frame of reference will be repealed while the light is moving back to the point.
Time between 2 points can only be measured correctly as one-way direction measurement and to do this then you need synchronized clocks.
Synchronization of clocks must be done in a different way than using light signals between them.
References
[1] “On the Electrodynamics of Moving Bodies, Albert Einstein, 1905”
(The theory of Special Relativity, English translation 1923).
http://www.fourmilab.ch/etexts/einstein/specrel/www/
This edition of Einstein’s “On the Electrodynamics of Moving Bodies” is based on the English translation of his original 1905 German-language paper (published as Zur Elektrodynamik bewegter Körper, in Annalen der Physik. 17:891, 1905) which appeared in the book The Principle of Relativity, published in 1923 by Methuen and Company, Ltd. of London. Most of the papers in that collection are English translations by W. Perrett and G.B. Jeffery from the German Das Relativatsprinzip, 4th ed., published in 1922 by Tuebner.
[2] “Relativity The special and general theory, Albert Einstein, 1916”
Translated by Robert W. Lawson. New York – Henry Holt and Company, 1920
[3] “University Physics (with Modern Physics), Young and Freedman. “
Sears and Zemansky’s 13. Edition, 2012
“I dare you to find any errors or prove the logic wrong. It should be very easy if Einstein’s 1. postulate is correct. If you can, then please send your prove to: “stjerne” at “relativitytheory.eu”
Danny Stoltenberg Stjerne, Denmark